학습목표
이번 강의에서는 Least Squares Problem에 대한 소개와 함께 앞으로 Least Squares를 배우는데 필요한 개념들을 배워보도록 하겠습니다. 벡터와 관련된 이 개념들은 선형대수에 있어 중요한 개념이니 꼭 알고 가시면 좋을 것 같습니다.
핵심 키워드
- 내적(Inner Product, Dot Product)
- 벡터의 길이(Vector Norm)
- 단위벡터(Unit Vector)
- 직교벡터(Orthogonal Vectors)
학습하기
앞서 배웠던 Over-determinded Linear System을 떠올려봅시다. 방정식의 수가 변수의 수보다 많을 경우에는, 적은 수의 변수로 많은 상황을 설명할 수 있어야한다는 뜻이니까, 해가 존재할 수 없었습니다.

이러한 연산을 위해 Matrix equation을 통해 표현할 수도 있었습니다.

Span을 통해서 설명하면, a1, a2, a3 세 개의 벡터로 Span할 수 있는 공간안에 b가 들어간다면, 해가 존재하는 것인데, 주어진 벡터로 Span할 수 있는 공간은 굉장히 얇은 초평면이 될 것이기 때문에, 해가 존재하지 않는 것입니다.

그러면 해가 없을 때(Over-determined system에서), 어떻게 해야하는가. 근사적으로라도 해를 구해봐야하는 거죠. 그러면 어떤 근이 가장 적절한가-라는 생각을 해야겠죠

이를 위해 기본적으로 내적(Inner product, Dot product)를 이해해봅시다. n차원의 벡터 u,v가 주어졌을 때, u와 v의 내적은 u.T * v로 정의됩니다.

이러한 내적은, 아래와 같은 성질을 갖습니다. 특히 마지막 응용이 중요하게 쓰일 수 있겠죠. 보시면 아시겠지만, 이러한 성질은 Linear한 성질과도 연결됩니다.

Vector의 Norm이란 건, Length라고 생각하시면 직관적입니다. (3,4)라는 벡터의 Norm은 보통 5라고 표현하죠.

구체적으로, 원점으로 부터 해당 벡터의 거리를 Norm이라고 칭합니다. 그리고 어떤 스칼라를 벡터에 곱한다 함은 그에 맞게끔 길이를 단순히 늘려주는 개념으로 보시면 되겠습니다.

이런 스칼라곱을 통해, 어떤 벡터든 길이가 1이 되게끔 스케일링을 할 수 있는데요. 이렇게 길이를 1로 바꿔주는 과정을 Normalizing이라고 하고, 길이기 1인 벡터를 Unit vector라고 칭합니다.

이제 벡터 간의 거리를 생각해봅시다. 벡터사이의 거리 dist(u,v)는 u-v의 Norm으로 정의됩니다. 고등과정에서 했던 내용과 유사합니다. 다만 그 당시에는 2차원에서만 생각했었고, 지금부터는 n차원으로 확장하는 것 뿐이겠죠.

이것의 기하학적 의미는, 아래 그림과 같이 평행사변형을 그림으로써 알 수 있겠습니다.

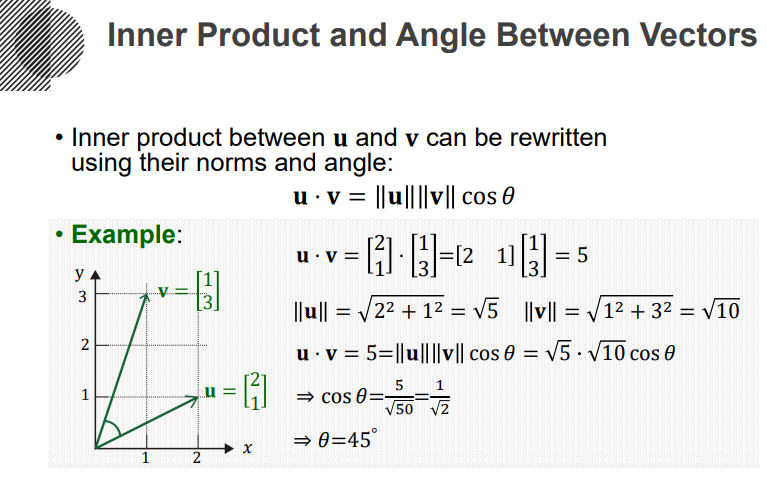
그리고 내적을 통해 두 개 벡터간의 각(Angle)을 계산할 수 있습니다. 이또한 고등과정의 수식을 사용하시는 것으로 충분합니다.
이제 굉장히 중요한 개념입니다. Orthogonal이라는 말은 수직으로 받아들이시면 됩니다. 두 개의 벡터가 Orthogonal하다는 말은 수직이라는 말이니까, 내적을 통해 구한 각이 90이 나오겠다는 말이되겠죠. 즉 두 벡터의 내적 값이 0라면, 수직인겁니다.

자 지금까지 선형변환-벡터노름-거리-내적을 배웠습니다. 꼭 내용을 기억해 두시고, 다음 내용으로 넘어가시면 되겠습니다.

이제 저희가 목표로 했던 Least square을 이해하기 위해, Over-determined system을 떠올려보죠. 아래와 같은 그림은 Over-determined가 아니죠. 그냥 역행렬을 계산하면, 유일해를 찾을 수 있습니다.

아래 그림과 같이 3개의 변수로 4개의 방정식을 설명해야하는 경우가 Over-determined입니다. 이 경우, 앞에서 찾았던 해를 일단 대입해서, 실제 y와 계산된 y를 뺏을 때 나오는 값을, Error로써 사용해볼 수 있습니다.

또 아예 새로운 x를 가져와 볼 수 있겠죠. 가져온 x를 가져와서 실제 y(=b)와 비교를 해보면 Error를 명확히 볼 수 있죠.

그럼 이러한 2개의 x후보 중에 어떤 것이 더 나은 솔루션인가? 를 정량적으로 계산해보죠.

여러 가지 방법이 있습니다만, 가장 자주 사용되는 것이 Sum of squared error입니다. 각각의 Error들을 제곱해서 더하고, 루트를 취하는 방법입니다. 이렇게 계산된 Total error를 보시면, 그냥 찍어넣은 x가 더 좋다고 말할 수 있겠습니다. 이제 저희가 하고 싶은 건, 이러한 Total error를 최소화하는 어떤 x를 찾아내는 것이 됩니다.

즉, 어떤 Over-determined system에서 Least squares solution이라는 건, 어떤 Least sqaured error를 최소화하는 x를 의미하게됩니다. Error = ||b-Ax|| 를 최소(min)화할 수 있는, x를 arg로 가져오는 거죠. 이런 x를 계산하는 문제를 Least square problem이라고 하고, 이제부터는 이런 문제를 어떻게 풀 것인가-에 대해 배워보도록 하겠습니다. 이상입니다.

'머신러닝 > [인공지능을 위한 선형대수]' 카테고리의 다른 글
| 정규방정식 (0) | 2020.05.18 |
|---|---|
| Least Squares와 그 기하학적 의미 (0) | 2020.05.17 |
| 전사함수와 일대일함수 (0) | 2020.05.15 |
| 선형변환 with Neural Networks (0) | 2020.05.14 |
| 선형변환 (0) | 2020.05.13 |



