학습목표
이번 강의에서는 벡터들 간의 선형결합에 대한 개념과 벡터공간 상의 Span의 개념에 대해 알아보겠습니다. 그리고 선형결합과 관련하여 네 가지의 새로운 관점을 통해 행렬의 곱셈을 심도있게 배우는 것을 목표로 합니다.
핵심 키워드
- 선형결합(Linear Combination)
- 생성(Span)
- 행렬의 곱셈
학습하기
이번에는 선형결합(Linear combination)입니다. 아래와 같이 여러 개의 벡터가 주어졌을 때, 이들에게 각각의 계수 또는 가중치를 곱해주고, 모두 합친 형태를 선형결합이라고 합니다. 만약 벡터가 3차원이라면, 선형결합도 3차원 벡터로 표현되겠죠.

앞서서, 선형시스템을 살펴봤었는데요. 아래 그림에서 Ax = b처럼, 행렬을 통해서 표현했었죠. 이번에는 선형결합을 사용해서 표현할테니, a1x1 + a2x2 + a3x3 = b 라는 방식으로, 벡터를 통해 표현될겁니다. 그리고 이런 형태를 벡터 방정식이라고 합니다. 이런 벡터 방정식으로 통해서 저희는, 공간적인 개념을 획득할 수 있게 되는데요.

그 중 하나가 Span입니다. Span이라는 건, 주어진 벡터들의 선형결합으로 표현되는 모든 벡터들의 집합을 의미합니다.

그러면, 이러한 Span은 기하학적으로, 공간적으로 어떤 의미를 갖는 지 생각해봅시다. 아래 그림을 보면 v1과 v2라는 2개의 벡터를 선형 결합하면, 하나의 평면(Plane)을 생성할 수 있게되죠. 이런 생각을 확장한다면 3개의 독립 벡터로는 하나의 Cubic같은 공간(사실상 3차원 공간 전체)을 생성할 수 있습니다.
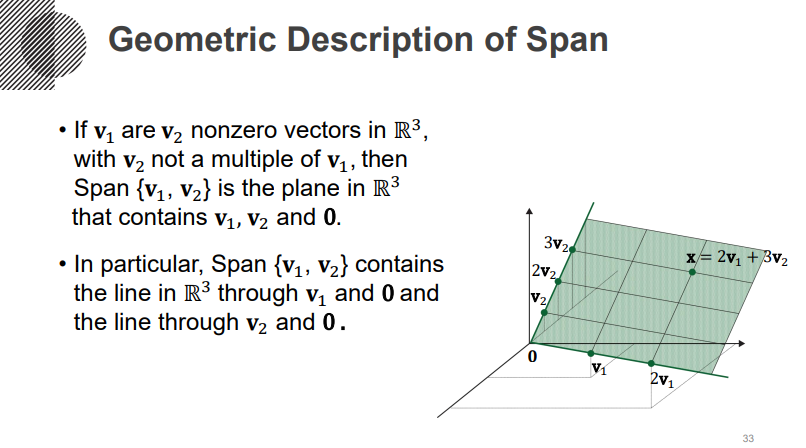
이러한 개념으로 벡터 방정식을 다시 들여다봅시다. 전체 공간이 3차원인데, 내가 가진 벡터는 2차원이라면, 이런 벡터를 아무리 선형결합한다한들, 3차원 공간 전체에 매핑될 수는 없어요. 이 말이 무슨말인가하면, 정확한 해를 구하지 못할 수 있다는 말입니다. 어떤 벡터들을 선형결합해서 만든, Span된 그 공간 안에, b라는 값이 존재해야 Solution이 존재할텐데, 내가 Span할 수 있는 공간은 전체 차원에 비해서 굉장히 조그마하니, b가 그 공간안에 있을 확률은 굉장히 적어지는거죠. 그러니까, 주어진 벡터로 Span된 공간 안에 b가 속할 때, Solution은 존재하는 겁니다.

이번에는 다시, 행렬의 곱연산을 이해하는 4가지 시각에 대해 알아보겠습니다. 이 또한 굉장히 중요한데요. 저희가 행렬간 연산을 진행한다는 말은, 두 개 벡터간의 행렬 연산을 따로따로 진행하는 셈입니다. 그런데 이게 굉장히 번거롭죠. 행렬의 쌍마다 따로 따로 계산을 하면, 두 개 행렬의 사이즈가 커질수록, 복잡도가 굉장히 늘어날테니까요. 그래서, 이걸 한 번에 계산되게할 방법이 없을까-에 대해 생각해봅시다. 벡터 방정식이 그 Key가 될 겁니다.

기본적인 행렬 곱연산을 생각해보면, 이들은 아래와 같이, 결국 선형결합으로 표현할 수 있겠죠. 보시면 x,y는 같은 벡터에 계수만 변화시켜 구성됩니다.

앞 선 방법은 Col을 기준으로 한 연산이었는데, 똑같이 Row에 대해서도 생각해볼 수 있겠죠. (Ax).T = x.T * A.T 라는 점에 주목하면 아래와 같이 정리될 수 있습니다.

마지막으로, 외적(Outer product)로 표현하는 방법입니다. [a c] * [b d].T = a*b + c*d 에서 a b c d 각각이 벡터가 됬을 뿐입니다. 중요한건 좌변과 우변이 equal이라는 점이죠. 좌변에서 우변으로 가는 것도 분명 중요하지만, 추후에는 우변에서 좌변으로 가는, 큰 행렬을 2개의 저차원 벡터 2개로 표현할 수 있다라는 그 개념을, Word2Vec, PCA, SVD 등 많은 부분에서 사용하게 될 겁니다. 그리고 머신러닝을 하다보면 Gaussian이란 이름을 자주 접하시게 될텐데, Covariance matrix in multivariate Gaussian, Gram matrix 등에도 이 Sum of (Rank-1) Outer products의 개념을 사용하시게 될겁니다. 이상입니다.

'머신러닝 > [인공지능을 위한 선형대수]' 카테고리의 다른 글
| 부분공간의 기저와 차원 (0) | 2020.05.13 |
|---|---|
| 선형독립과 선형종속 (0) | 2020.05.12 |
| 실습 1 (0) | 2020.05.10 |
| 선형방정식과 선형시스템 (0) | 2020.05.09 |
| 선형대수의 기초 (1) | 2020.05.08 |


