앞서 인접 행렬, 라플라시안 행렬 등을 말씀드리면서, 그래프를 예쁘장하게 표현한 저런 행렬들은 기본적으로 사이즈가 너무 크다는, 큰 단점이 있다. 때문에 그래프 임베딩을 통해 조금 더 저차원에 정보를 압축해 사용한다- 고 말씀드렸습니다. 그런 그래프 임베딩은 어떤 방식으로 학습되는지, 그리고 어떤 방법론들이 제시되었는지- 에 대해 정말 간략히 정리해두겠습니다. 참고로 아래 내용은 모두 NLP에서의 임베딩 방법론에 대한 지식이 어느정도 있는 것을 가정하고 작성하였습니다.
A. Deepwalk: Online Learning of Social Representations (2014)
2014년에 발표된 논문입니다. 여기서 등장하는 임베딩은 NLP에서의 임베딩 방법론과 크게 다르지 않습니다. 정확히는 Word2Vec과 거의 같습니다. Word2Vec에서는 한 문장 안에 등장하는 여러 단어들 사이의 관계를 CBOW, Skip-gram 등의 구조로 학습하게 되는데, Deepwalk 임베딩은 문장을 Walk로, 단어를 Node로 매칭하여, 그래프에서의 Word2Vec을 시행합니다. 갑자기 등장한 Walk가 애매할 수 있는데, Word2Vec을 좀 더 뜯으면, 어떤 책 안에 있는 단어들을 학습할 때, 일단 문장 단위로 나누고, 그 문장 한 줄 한 줄을 인풋으로 사용해서 임베딩 값을 획득합니다. 저희는 책 대신 그래프를 뜯어야되는데, 그래프의 문장은 대체 뭘까- 를 깊이 고민해야합니다. 물론 다른 방법도 있지만, 해당 논문에서는 Walk를 그래프의 문장으로 매칭합니다. 이게 끝이에요. 그 다음부터는 Word2Vec의 Skip-gram 구조로 학습하고, 임베딩값을 뜯어낸다. 그랬더니 뭐 결과가 좀 괜찮더라. 이정도입니다.
B. Node2Vec: Scalable Feature Learning for Networks (2016)
2016년에 발표된 논문입니다. 이건 Deepwalk를 조금 발전시킨 정도, 라고 생각합니다. 앞서 Walk를 가져와서 임베딩값을 끄집어 내는데, 이런 Walk를 조금 더 깊이 생각해보면, 고민해야할 거리가 꽤나 많습니다. 이걸 몇 개를 설정해야할까, 이 놈의 길이는 얼마로 잡아볼까, 임마 길이가 40이라면, Depth를 깊이 가져오는 놈을 잡아줘야할까, Breadth를 깊이 가져오는 놈을 잡아줘야할까... 등이 있겠지요. 해당 논문에서는 저 Depth와 Breadth에 조금 집중했습니다. 느낌적인 느낌 느낌을 생각해보면, Breadth를 깊이 가져온다는 말은, 시작 노드 근처에 있는 노드들을 주욱 가져온다는 말이고, 이건, 시작 노드의 이웃에 대한 정보를 주로 가져온다- 라는 뜻이겠네요. 즉, 비슷한 임베딩 값을 갖는 노드들은 비슷한 이웃을 가진다- 이런 목적을 가진 임베딩 방법이 되겠습니다. 반대로 Depth를 깊이 가져온다는 말은, 시작 노드로부터 타고 타고 계속 타고 올라가니까 와 이런 놈이랑도 관계가 있구나- 라는 정보를 가져오게 될텐데, 이걸 본 논문에서는, 노드의 구조적 역활(Structural role)에 초점을 맞추는 것이다- 라고 설명합니다. (고급지게 Structural equivalence,,.) 개인적으로 Breadth에 비해 Depth는 조금 이해가 안되었는데, 아래 시각화 결과를 보면 대충 맞기는 한,,. 것 같기는 한데 확신까지는 들지 않네요.

쨋든 이런 Depth와 Breadth. 둘 다 적용해서 모든 정보를 끌고오면 좋을 것 같은데, 우선순위를 배당할 수 밖에 없는 문제이기 때문에, 데이터별로, 목적별로 그 비율을 조정해서 사용해야합니다. 이걸 파라미터로 구현한게 Node2Vec이네요.
C. SDNE: Structural Deep Network Embedding (2016)

이 논문도 2016년 발표됬네요. 다만 앞의 Walk를 통해 임베딩을 끌고오는 앞선 2개의 방법과는 궤가 좀 다르네요. 위의 그림이 SDNE의 핵심 포인트를 가장 잘 설명하고 있는 것 같습니다. 구조를 보면 Autoencoder와 같습니다. 그림 상의 Autoencoder 2개는 파라미터를 공유하는 1개의 Autoencoder지만, 편의상 1번 Encoder, 2번 Encoder라고 지칭하겠습니다. 저기서 Encoder의 Input, Output부터 생각해보면, 얘들은 인접 행렬의 한 행이 들어가요. 이걸 Encoder loss로 학습시키면, 중간에서 임베딩 값을 얻을 수 있습니다. 그리고 인접 행렬의 한 행은 한 노드에 대한 정보이고, 이건 구체적으로 해당 노드의 이웃들에 대한 정보입니다. 그럼 Encoder로 얻어지는 임베딩은 해당 노드의 이웃에 대한 정보에서 추출되니 Local structure를 보존한 값입니다. 그리고, 이렇게 얻어진 2개 임베딩값끼리 거리를 계산해서, 비슷한 임베딩 값이면(=비슷한 이웃을 갖는 노드라면), 둘 사이의 거리를 좁히게끔 학습(Laplacian Eigenmaps를 사용)하면, 최종적으로 얻어진 임베딩을 2차원 평면에 투영하면, 비슷한 노드들은 지들끼리 모여있고, 다른 노드들은 좀 멀리 떨어지게끔, 그렇게 시각화됩니다. 즉, Global structure도 보존할 수 있는 셈이네요. 해당 논문에서는 Node2Vec 보다 SDNE 짱짱맨이라는데, 다른 조사 논문들을 읽어보면 역시 상황마다 다르다-로 정리가 되는 것 같습니다.
이 외에도 정말 다양한 임베딩 방법론이 존재하는데, 지금부터는 요 논문(2018)-을 참고하여, 간략하게만! 정리해보겠습니다.

우선 지금부터 가볍게 다뤄볼 임베딩의 종류는 위 테이블과 같습니다. Factorization 기반이라는 말은, 추천 시스템에서 SVD같은 방법론으로 Latent factor를 고려한 행렬을 추출했던 것을 떠올리시면 얼추 맞습니다. 이 때도 고차원의 데이터를 저차원으로 매핑하는 임베딩의 역활을 진행했었습니다. 쨋든 여기서는 Adjacency matrix, Laplacian matrix, Node transition probability matrix, Smilarity matrix 등을 이용합니다. Random walk 라는 말은, 그래프의 특징을 잡아내기 위해 Walk를 사용했다. 이 방법은, 전체 그래프는 모르고 부분만 알고 있을 때나, 그래프가 너무 커서 전체를 측정할 수 없을 때 유용합니다. 모든 가능한 Walk를 다 사용하는게 아니라, Random walk 몇개 뽑아서 사용하거든요. Deep learning 기반이라는 말은, Laplacian matrix 등으로 부터 Autoencoder와 같은 딥러닝 구조로 임베딩을 추출했다. Miscellaneous는 잡다한- 이라는 뜻이라는데, Factorization과 비슷하면서도 조금 독특한 구조를 띄고 있습니다. 2018년에 발표된 논문인 탓에 나름 네임드 임베딩인 Anonymous Walk Embedding(AWE, 2018)이 같이 비교되지 못한게 아쉽네요.
추가로 Properties preserved에 대해 간단히 설명드리면, 1st order proximity는, Edge weight 그 자체에 대한 정보입니다. 두 개의 노드가 있을 때, 이 노드를 이어주는 엣지의 Weight가 클 수록, 관계가 깊은 노드인데 이런 정보를 보존하겠다는 겁니다. 2nd order proximity는 노드 둘만의 Edge weight로 노드의 관계를 정리할게 아니라, 각각의 노드와 연결된 이웃들이 얼마나 비슷한지, 를 보고 관계가 깊은지 얕은지를 판단하겠다는 거구요. 3rd, 4th, ... 로 가면 그렇게 점점 더 깊은? 정보를 보존하겠다는 의미입니다.
1.1. Locally Linear Embedding (LLE)
LLE는 단순한 Dimention reduction 모델로도 등장하는 놈입니다. 이 친구는, 모든 노드는 그것의 이웃 노드들의 선형 결합으로 구성될 것이다- 라는 단순한 가정을 기반으로 둔 놈이며, 가장 낮은 아이젠밸류에 대응하는 아이젠벡터를 날려버린다는 것과 내용이 동일합니다. 아래 수식을 최소화하는 방향으로 학습하게 됩니다.

1.2. Laplacian Eigenmaps (LE)
SDNE에서도 등장하는 해당 임베딩은, Edge weigh가 높을 수록 두 노드간의 거리가 가까워질 수 있는 것에 집중한 방법론입입니다. Normalized laplacian matrix를 기반으로 계산되며 아래 수식을 최소화하는 방향으로 학습하게 됩니다.

1.3. Cauchy graph embedding
Laplacian eigenmaps의 손실 함수를 조금 수정한 놈입니다. 앞선 손실 함수가 단순 Quardratic penalty function을 사용하기 때문에, 노드간의 유사성 보다, 비유사성을 더 강조하게된다는 문제가 있었는데, 이러면 다른건 다르다고 말하는데, 비슷한 것=붙어있는 것에 대한 정보는 조금 흐리멍텅하게 전달시키다 보니, Local topology가 잘 보존되지 않는다는 단점이 있었다는 거지요. 그래서 수식을 조금 수정해서, 요 수식을 최대화하는 방향으로 학습을 시킵니다.
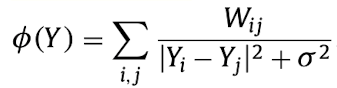
1.4. Graph Factorization (GF)
이름 그대로, Adjacency matrix를 Factorize하는 모델로, 최초로 그래프 임베딩의 계산 복잡도를 O(|E|)로 끌어올렸습니다. 아래와 같은 수식을 최소화하는 방향으로 학습하게 됩니다.

1.5. HOPE
앞선 기법들과는 달리 Similarity matrix를 활용해 Higher order proximity를 보존하는 기법입니다. 때문에 Similarity measure를 무엇으로 채택하느냐에 따라 성능이 달라지며, 임베딩의 효율성을 위해 SVD를 접목했습니다.
2.1. Deepwalk
위에 있으니 생략합니다.
2.2. Node2Vec
위에 있으니 생략합니다.
2.3. Hierarchical representation learning for networks (HARP)
Deepwalk와 Node2Vec의 경우, 목적 함수가 Non-convex라서, Local optima에 빠질 수 있었는데, HARP는 이를 개선하기 위해, 조금 더 개선된 Weight initialization을 적용했습니다. 이를 위해 노드의 계층적 정보를 활용했고, 앞선 두 개의 방법보다 조금 더 나은 결과를 보입니다.
2.4. Walklets
Deepwalk와 Node2Vec은 Random walk를 이용해 Implicitly한 방법으로 Higher order proximity를 보존했습니다. 그러니까 랜덤성이 개입할 수 밖에 없는데, Factorization 기반 방법들은, 그런거 없고 Explicitly하게 특성을 보존했습니다. Walklet은 Random walk를 이용하되, Explicitly하게 특성을 보존하길 원했고, 그래프의 특정 노드들을 Skip하는 방식으로 모델링했습니다.
3.1. Structural deep network embedding (SDNE)
위에 있으니 생략합니다.
3.2. Deep neural networks for learning graph representations (DNGR)
해당 모델은 Random surfing, Positive pointwise mutual information(PPMI) calculation, Stacked denoising autoencoder 라는 3가지 요소로 구성되어있습니다. Random surfing은 HOPE의 Similarity matrix와 유사하게, Probabilistic co-occurence matrix를 생성하기 위해 Input graph를 사용하며, 이렇게 만들어진 행렬은 PPMI 행렬로 변환되고, 그리고 Stacked denosing autoencoder를 통해 임베딩을 획득합니다.
3.3. Graph convolutional networks (GCN)
Adjacency matrix를 Input으로 활용하는 SDNE, PPMI matrix를 Input으로 활용하는 DNGR와 같은 Deep learning 기반 방법론들은, Global neighborhood를 사용해서 계산합니다. 이 말은, 사용하는 정보가 많다는 장점도 있지만, 계산비용이 높아지고, 계산이 비효율적일 수 있다는 큰 단점이 있습니다. GCN의 경우, 이런 단점을 해결하기 위해 제시된 모델로, 반복적인 Aggregating을 통해 노드의 이웃에 대한 정보를 수집하게 됩니다. Conv filter가 처음에는 Local feature부터 수집하기 시작해서, 그 반복을 더해갈 수록 Global한 feature를 배우게 되는 것 처럼, GCN의 Aggregating도 반복될 수록 Local한 것에서 시작하여 Global한 neighbors에 대한 정보를 임베딩할 수 있게 됩니다.
4.1. Large-scale information network embedding (LINE)
앞서 말한 것 처럼, 조금 잡종으로 섞어낸 친군데, 간략히 말하면 first-order proximities와 second-order proximities를 각각의 함수로 Explicit하게 지정하고, 이 두 함수(분포)의 차이를 Kullback-Leibler divergence를 통해 최소화하는 방식으로 학습됩니다. 그러니까, first-order를 생각해보면 GF 방법론(Adjacency matrix와 dot product of embeddings가 비슷해지도록 학습)과 비슷하게. 그러나 직접 하나의 목적 함수를 만들어 학습했던 것과는 달리, 앞서 말한 것 처럼 KL divergence를 통해 분포를 유사하게 만드는 방식으로 학습합니다. second-proximities도 first-proximities와 거의 동일합니다. 더 자세한 설명은 이 분이 잘 해놓으셨으니 참고하시면 좋을 것 같습니다.
5. Experiments and analysis
이런 다양한 방법론을 사용해서, 해당 논문에서는 다양한 과제를 수행했습니다. 대체적으로 Higher order proximities를 보존하는 방법론이 더 좋은 결과를 냈습니다만, 모든 상황에서 가장 최고의 결과를 도출하는 단 하나의 모델을 없었습니다.
5.1. Graph reconsturction
Higher order proximites를 보존하는 방법론이 다른 것들에 비해 훨씬 우위였습니다. Laplacian eigenmaps 같은 경우 1st order proximities 밖에 보존하지 못하기에 결과가 후졌지만, 반대로 데이터셋이 high order가 애초에 없는 경우, 다른 모델과 비슷한 성능을 보입니다. 인상 깊었던 것은 SDNE가 꾸준히 높은 성능을 보였다는 점. Node2Vec은 SDNE보다 높은 차원의 정보를 보존함에도 더 낮은 정밀도를 기록했는데, 이는 Node2Vec이 비선형적으로 정보를 넘기면서 비선형 매니폴드 공간을 학습했기 때문일 것이라는 점. 반대로 HOPE는 높은 차원의 정보를 선형적으로 넘기면서 Node2Vec보다는 좋은 정밀도를 기록했다는 점. 정도가 있었습니다.
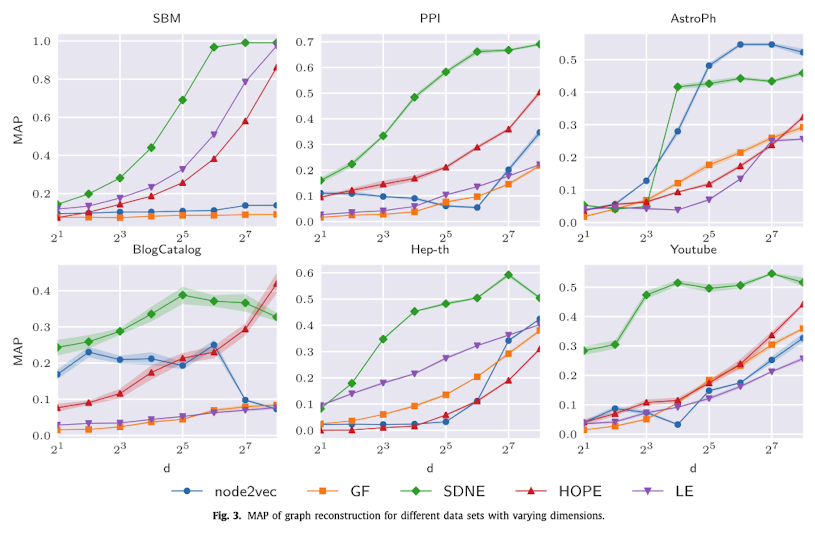
5.2. Link prediction
이번 과제의 경우, 특히나 데이터셋마다 좋은 성과를 달성하는 모델이 달랐습니다. Node2Vec은 BlogCatalog에서는 괜찮았지만, 나머지에서는 개똥이었고, SDNE, HOPE는 대체적으로 괜찮았습니다. 또 Graph reconstruction과는 달리, 임베딩 차원 수와 MAP가 별로 비례하지 않는 양상이 자주 등장했는데, 차원 수를 늘릴수록 관측된 링크들에 오버피팅되어 생기는 문제로 저자들은 판단했습니다.
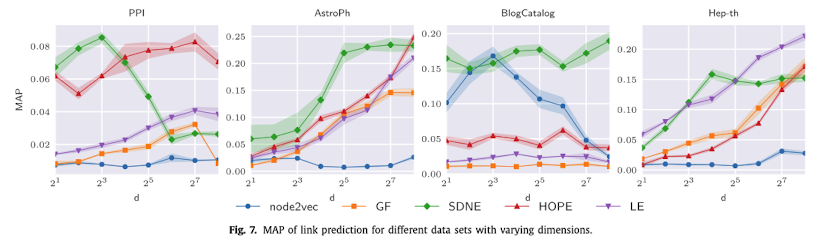
5.3. Node classification
이번 과제에서는 Node2Vec이 꽤나 좋은 결과를 보였습니다. Depth와 Breadth를 동시에 고려했던 특성탓으로 평가됩니다. 다만 단순한 데이터셋인 SBM에서는, 다른 방법들이 훨씬 좋은 결과를 보입니다. 이는 SBM에는 노드간에 Structural equivalence가 애초에 없다는 것으로 해석됩니다.

6. Conclusions
대표적으로 실험했던 위의 5가지 모델(SDNE, HOPE, Node2Vec, GF, LE)를 비교해보면 결국 아래의 표와 같이 정리되네요. 그래프 구조에 로버스트한 모델은 SDNE, Node2Vec. Task마다 튜닝할 수 있는 여지가 많은 것은 SDNE, Node2Vec, 귀찮은 하이퍼 파라미터 설정을 할게 거의 없는건 HOPE, GF, LE. 하이퍼 파리미터 민감도가 좀 낮은 것은 LE, 거대한 데이터도 잘 핸들링 가능한 모델은 HOPE, Node2Vec, GF, LE.
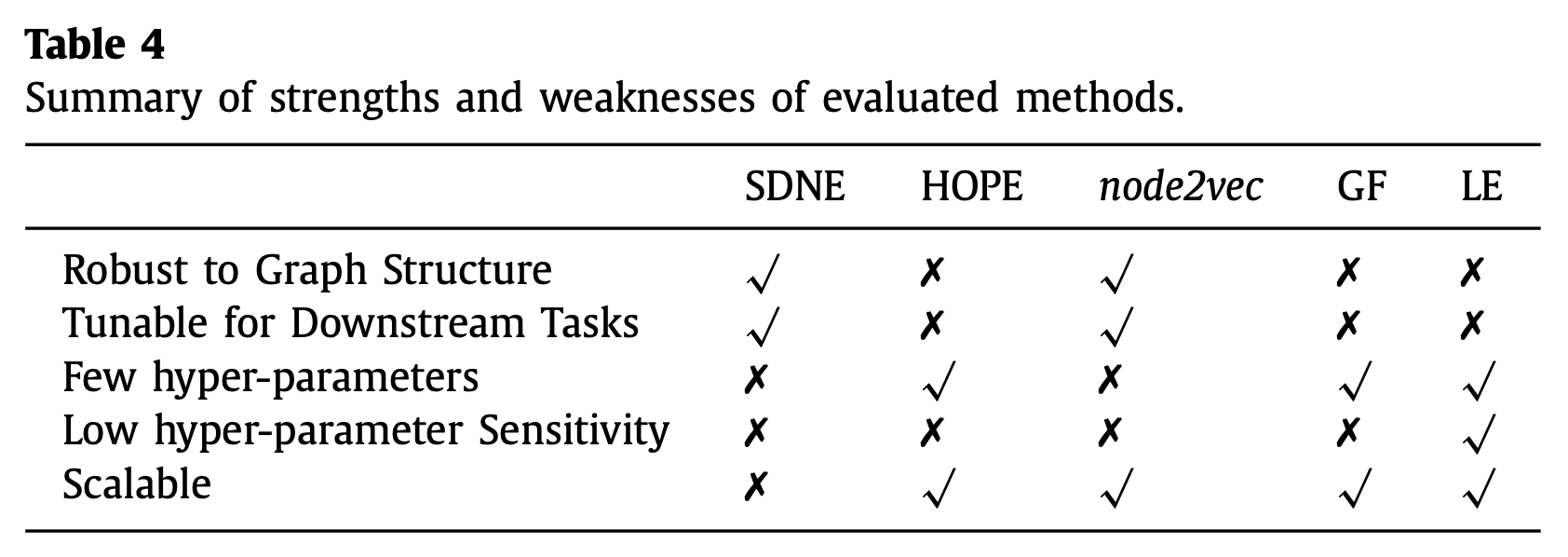
위의 실험결과를 종합해보면, SDNE는 엥간해서 좋지만, 내가 어떻게 튜닝할지에 따라 성능이 왔다갔다하니, 내가 고생을 좀 해줘야하고, Node2Vec은 Node classification에서는 SDNE보다 강력하게 사용할 수 있다. HOPE는 간단하게 세팅해서 사용할 수 있지만, 데이터셋에 많이 휘둘린다. 정도인 것 같습니다.
'머신러닝 > [기타]' 카테고리의 다른 글
| Precision at k(Pr@k), Average Precision(AP), Mean Average Precision(MAP) (0) | 2020.09.07 |
|---|---|
| Non-local self-similarity (0) | 2020.09.06 |
| 그래프와 인접 행렬, 라플라시안 행렬(Adjacent matrix, Laplacian matrix) (4) | 2020.09.04 |
| CNN의 흐름? 역사? (0) | 2020.09.02 |
| Universal Approximation Theorem, UAT (0) | 2020.06.17 |

